※本記事は、NorthDetail Advent Calendar 2020の一環として投稿しています
こんにちは、eiyuuです。
最近AWS DeepRacerに取り組んでいます。
その中で、そこそこ使えそうなアプローチが1つ見つかりましたので、紹介しようというのが本記事の主旨です。
ズバリ、「コースを"効率的"に走破することができる経路を計算し、その経路に沿うように学習させる」です。 本記事ではその経路のことを「レーシングライン」と呼ぶことにします。
つまるところ図1のような経路を計算してそれに沿わせるということです。"効率的"が何を指すかには諸説ありますが、そのいくつかの基準を後で提案します。
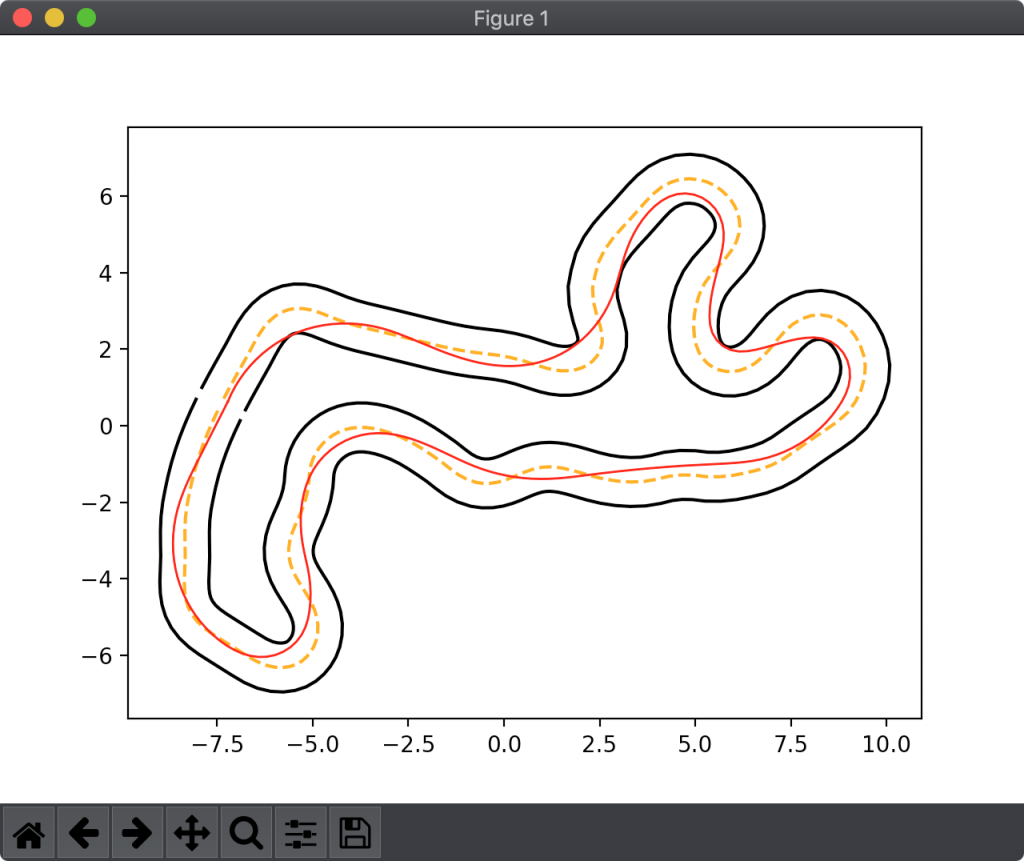
AWS DeepRacerにおける基本中の基本とも言えるアプローチとして、中心線に沿わせるというものがあります。
実際、このアプローチは安定して良い成果が得られます。まずは完走できるようなモデルを作りたいという場合には(実装のシンプルさも含めて)最適なアプローチの1つです。
一方DeepRacerリーグで毎月行われるレースで上位に入ろうとする場合には、1つの大きな弱点が目立ってきます。
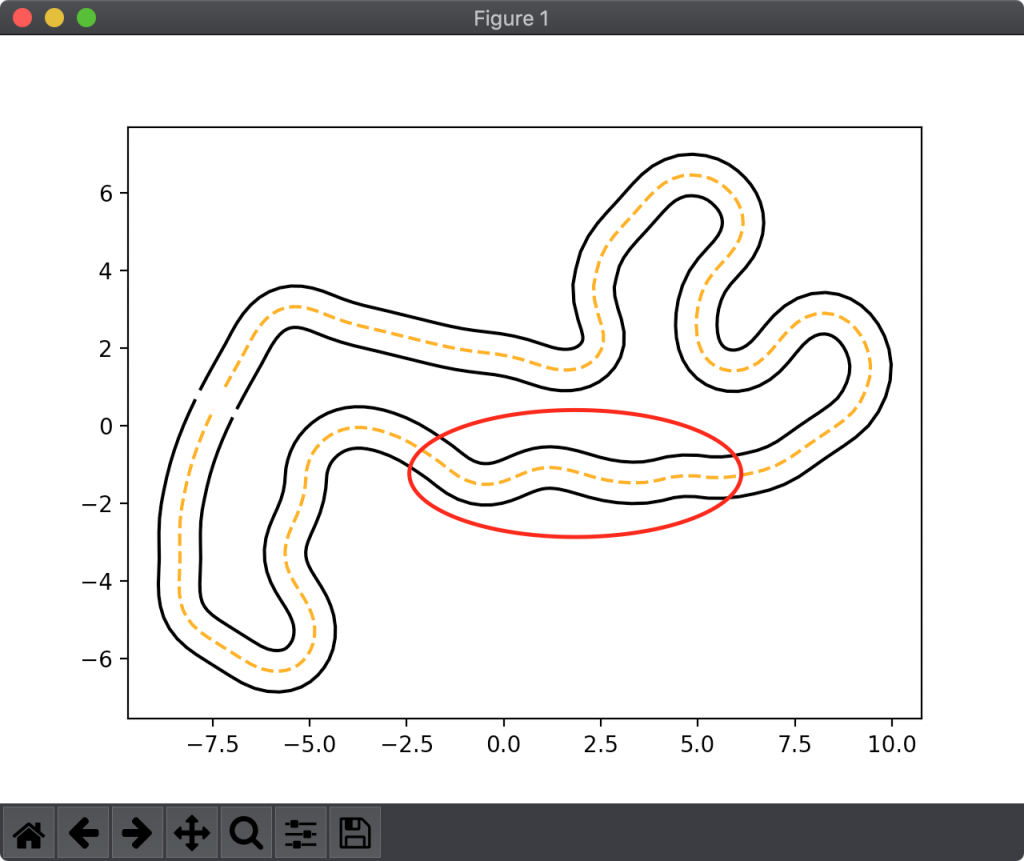
それは、まっすぐ進めるところでも律儀に曲がってしまうという点です。
図2の赤い丸で囲んだ部分を見てください。この部分は中心線に沿わずとも、直線的に進むことができるはずです。むしろ中心線に沿って進もうとすると何度も細かく曲がる必要が出てくるため、スピード・安定性の双方に悪影響を与え、結果としてタイムも遅くなります。
そのためレースで上位に食い込むためにはこのような部分を直進するような、例えば今回提案するようなアプローチが求められます。
さて、それではどうすればレーシングラインを生成できるでしょうか?
方法は1つに限られてはいませんが、今回は進化計算を使った方法でやってみます。 理由は、筆者が進化計算に触ったことがあってとっつきやすかったためです。 他の生成方法との比較は未実施です。
関数の最小値(or 最大値)とその時の引数を解析的ではなく探索的に解く手法の一分野です。筆者の理解に基づく説明なので、ググると別の説明が出てくると思います。
関数の厳密な式がわかっていて、且つ微分可能性などの条件が揃っている場合、解析的な方法を用いて最小値を求めることができます。
しかし、そうでない場合には解析的な手法ではなく探索的な手法を使う必要があります。
まず引数をランダムに複数生成して、それぞれの出力を調べる。そして出力の値が小さかった引数を選んで、その近傍からまた引数をランダムに複数生成する。そして出力の値が小さかった引数を選んで、、、という流れで探索を進めていきます。これが(ダーウィンが言うところの)生物の進化(自然淘汰)の様子と似ていることから進化計算と呼ばれます。
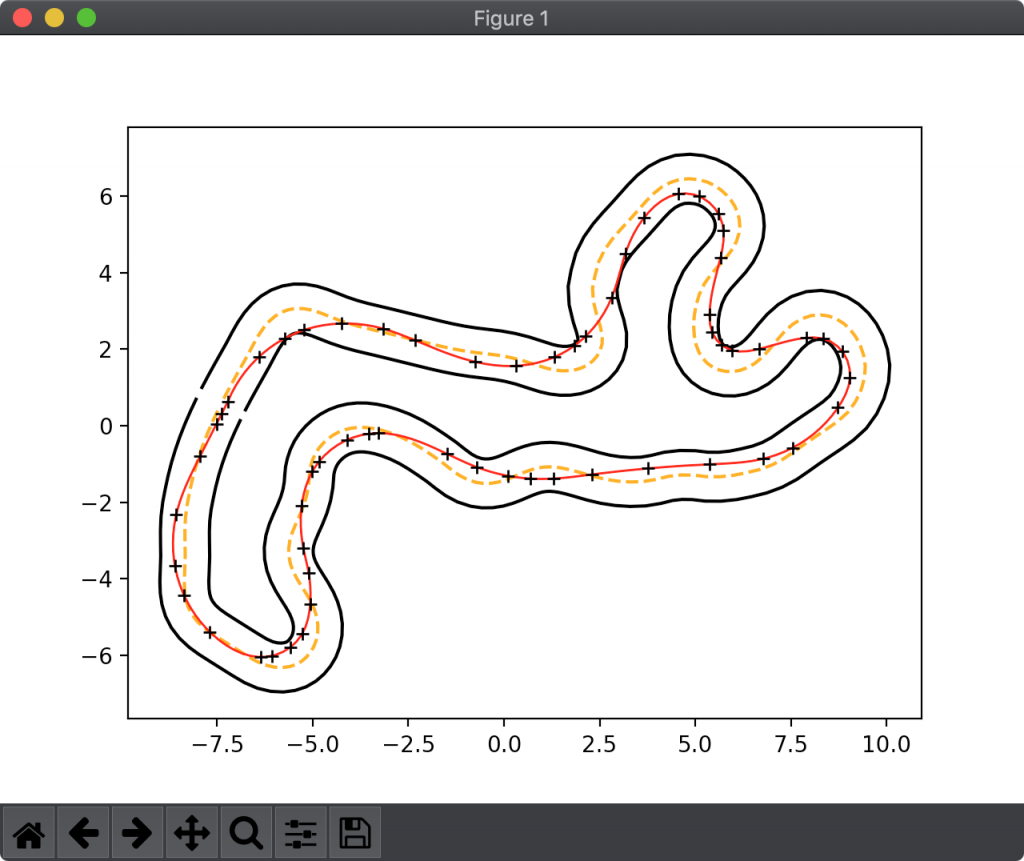
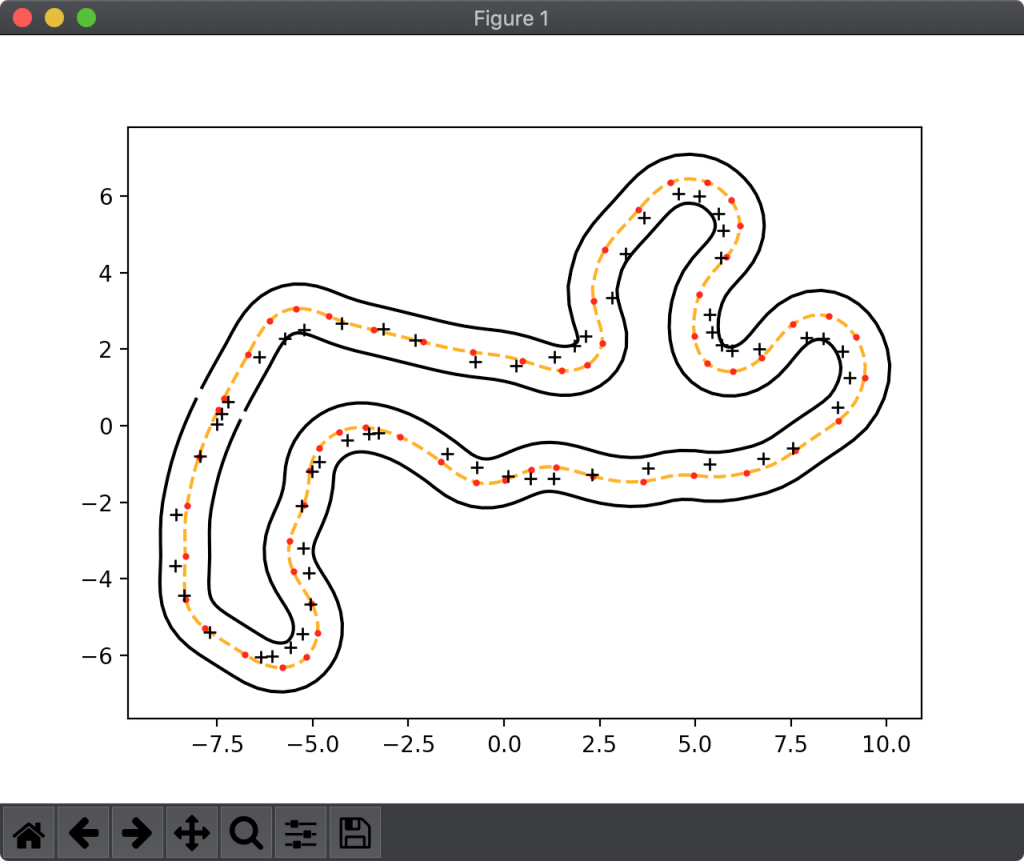
まず、レーシングラインを有限個の制御点から生成されるスプライン曲線であるとします。図1で示したレーシングラインも、実は図3に示すような制御点から生成されたスプライン曲線です。
次に、全ての制御点を入力として、そこから生成されるレーシングラインを評価する関数を考えます。評価が良いほど低い値、評価が悪いほど高い値をスカラーで返します。
評価が悪いほど高い値というのが少し直感に反するかもしれませんが、悪い部分にペナルティを与えて行って、その合計値を返すという様に考えるとわかりやすいと思います。
人間は良いところより悪いところを見つける方が得意だ、という進化計算考案者なりの皮肉なのだと思います。
あとは、この評価関数の最小値を得る制御点の組み合わせを進化計算を用いて求めれば良い、という寸法です。
先に述べた通り、評価関数の入力はレーシングラインを生成する制御点列です。今回は60個の点列とします。
各点の座標の表現にxy座標を用いると探索範囲が広すぎて進化計算がうまくいかなくなるので、少し座標の表現を工夫します。
まず、コースの中心線を60分割します。60は制御点の数と同じ値です。そして、i番目の制御点を、i番目の中心線分割点を中心とした極座標で表します。こうすることで、0 <= r < ({コース幅} / 2) -π <= θ < π の範囲でランダムに制御点を生成すれば、だいたいコースの形に沿った制御点列が得られることになります。
参考のために、図4に中心点分割点と制御点の位置関係を示しておきます。
評価関数の出力はレーシングラインの出来を決める肝となるところです。先に少し触れた通り、レーシングラインの悪い部分をいくつかの基準で判断して、そのペナルティを合計するという形をとります。
今回は以下に示す3つの基準を採用しました。
総距離が長いと当然ラップタイムは遅くなります。また、総距離が同じでもカーブより直線の方がスピードが出せるため、そう言った部分も考慮したものを理論上のラップタイムとします。
i番目の制御点とi+1番目の制御点との距離(メートル)をDi、i-1番目の制御点とi番目の制御点とi+1番目の制御点を通る円の半径(メートル)をRi、車が出せる最高速をVmaxとした時、i番目とi+1番目の制御点間を通過する時間Tiは以下の式で近似できます。
4.905はDeepRacerの車の特性から計算した定数です。
Ti = Di / min(sqrt(4.905 * Ri), Vmax)あとはこのTiを合計すれば理論上のラップタイムが計算できます。このラップタイムを秒単位で表したものを1つ目のペナルティとします。
経路上に急カーブが存在する場合、そこで急ハンドルを切ることになり、スピンの原因となります。そこで、カーブの曲率変化に対してペナルティを与えます。高い曲率に対してではなく、曲率の大きな変化に対して大きなペナルティを与えます。
i-1番目の制御点とi番目の制御点とi+1番目の制御点を通る円の半径の逆数をCiとします。ただし、右曲がりの時は負の値、左曲がりの時は正の値とします。
そして、CiとCi+1の差の絶対値をDCiとします。
このDCiの合計値を2つ目のペナルティとします。
各制御点が中心線分割点から離れすぎている時、コースからはみ出してしまうなど、不都合があります。
そこで、i番目の制御点と、それに対応する中央線分割点との距離がコース幅の半分を超えていた場合、超えた距離(メートル単位)をOiとします。 超えていない場合、Oi = 0 とします。
このOiの合計値を3つ目のペナルティとします。
上記3つのペナルティを重み付きで合計します。この重みも結果に影響してきますが、ここは試しながら決めていくしかありません。
k番目のペナルティの重みのWkとすると、度々図示してきたレーシングラインは、W1 = 1.0, W2 = 0.15, W3 = 1000 として生成したものです。
ペナルティの重みの違いによって生成結果にどのような変化が見られるか実験を行います。
ハンドル角の急激な変化をどれだけ問題視するかを軸として実験します。つまり、W2の値を増減させた際の変化を見ます。
進化計算のアルゴリズムには、CMA-ESを使い、10000世代まで計算しました。
筆者の環境(MacBook Pro / 2.4 GHz Intel Core i5)だと20分くらいで終わります。
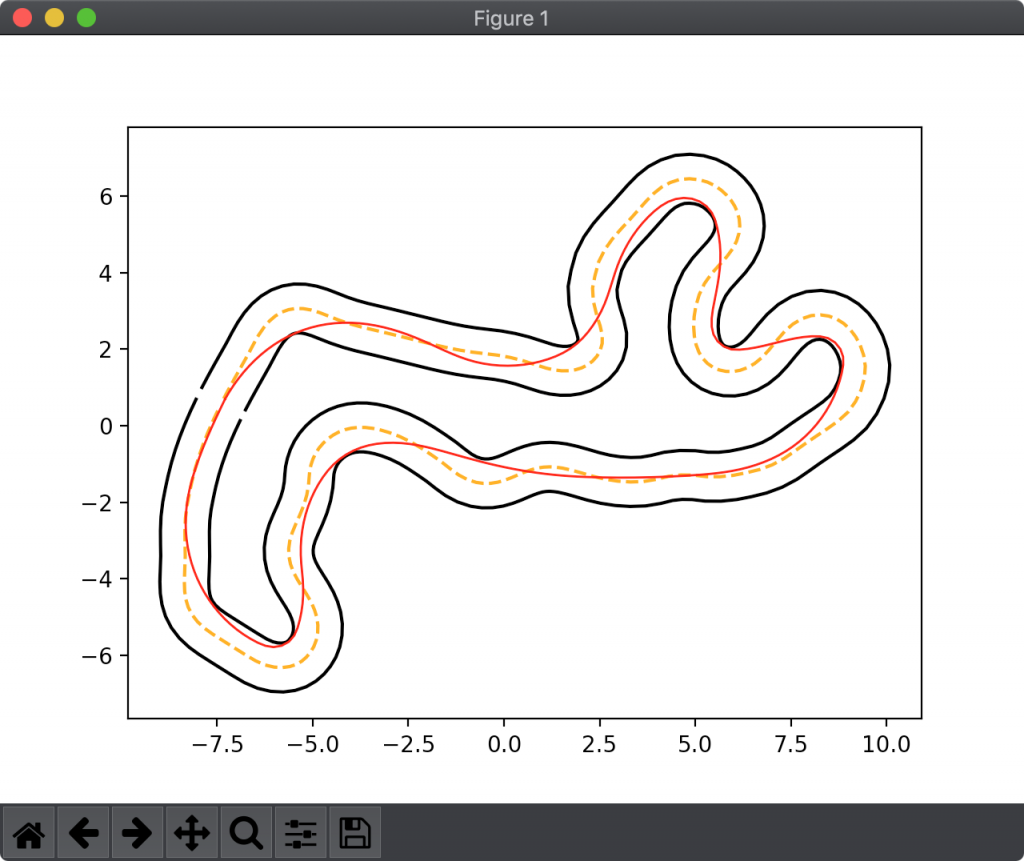
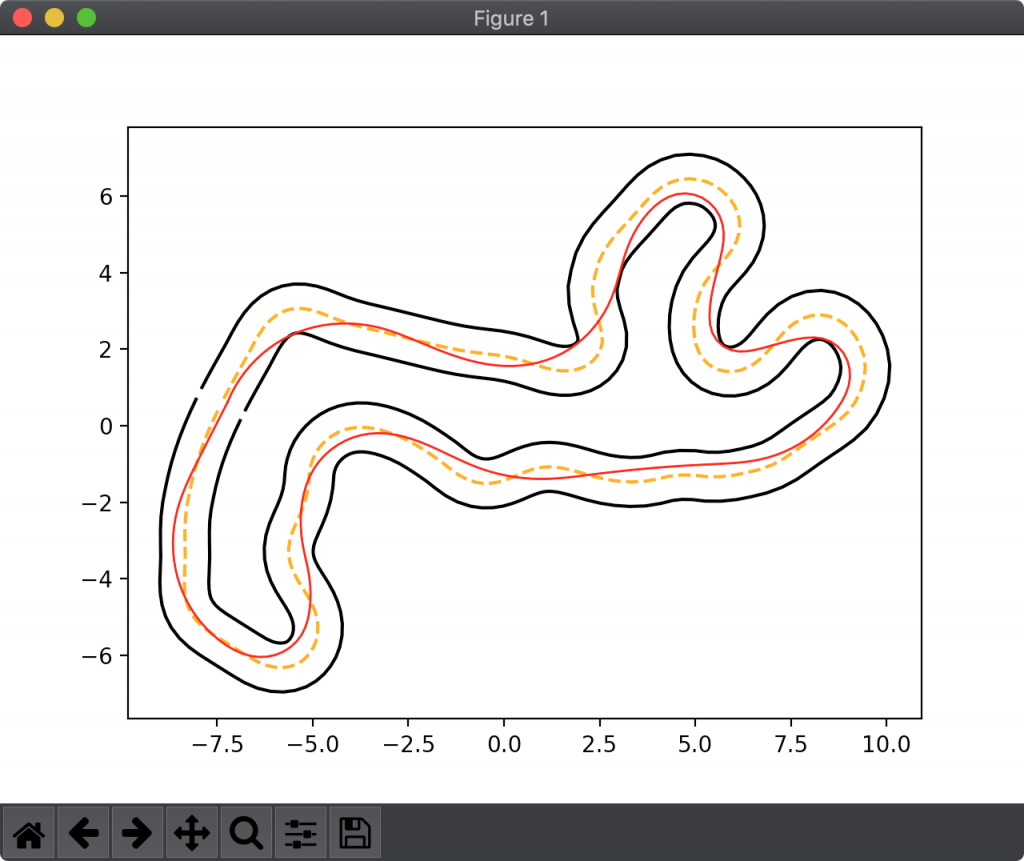
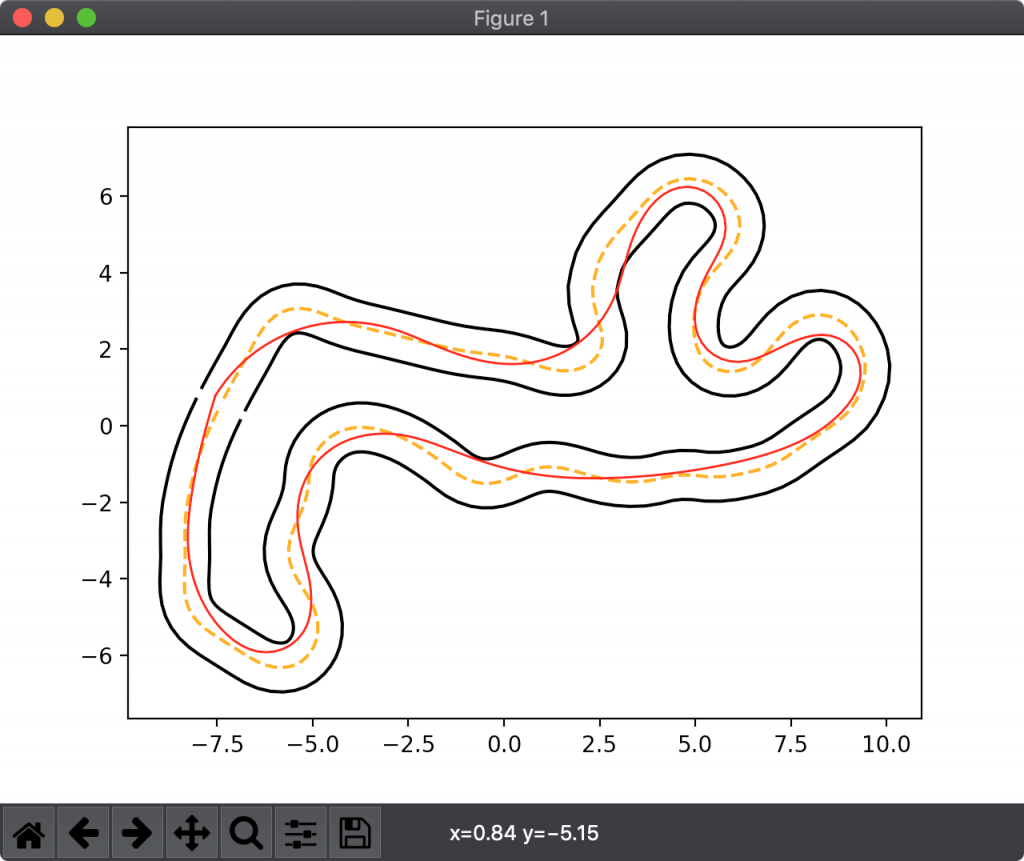
結果を図5〜7に示します。図5は W2 = 0.05 、図6は W2 = 0.15 、図7は W2 = 0.25 としました。
その他の重みは共通して W1 = 1.0, W3 = 1000 です。
図5は、急ハンドルをそこまで問題視せず、理論上のラップタイムがより短くなるようなラインを生成します。図6と比較して、急なカーブを中心に構成されていることがわかります。
図7は、急ハンドルをかなり問題視した場合の結果です。図6に比べて、タイムを犠牲にしてでも緩やかに曲がることを意識したラインになりました。タイムを犠牲にするとはいいましたが、安定性の関係で結局これが一番速い、なんてこともありうるのが悩ましいところです。
さて、図5〜7の中で結局どれが一番良いレーシングラインなのでしょうか?それは現時点では判断がつきません。
一つ一つ実際に学習させて、一番タイムの良かったラインが良いラインだったと判断して、次回以降に活かしていく(人間も一緒に学習していくのです)という落とし所になると思います。
最初は中心線に沿わせるサンプルの報酬関数と同じ考え方で、レーシングラインからの距離を計算して、閾値以上ならいくら、未満ならいくら、という考え方で良いと思います。
ただ、これだと少し安定しないのではないかという説がチーム内にあって、もう少し安定するやり方を考えて、形になろうとしているところです。
その際にはまた記事にできたら良いな、と思います。
当初は実装まで書く予定だったのですが、解説の時点で長くなりすぎたので、実装についてはまた別の機会で記事にしたいと思います。待ちきれないなんて人がもしいたら理論を読んでなんとか実装してください。
一応の情報として、Python3.8で実装しました。また、CMA-ESを実行するフレームワークとして、DEAPを利用しました。
本記事では、AWS DeepRacerの報酬関数として、「レーシングラインに沿わせる」というアプローチを提案しました。また、そのための、進化計算を用いたレーシングラインの生成方法について解説しました。実装については、また別の機会に実装編として記事にしたいと思います。