あるテーマに対して言語化された情報(問題、意見、データなど)を1つ1枚のカードに書き出し、類似するカードを集めて中項目、大項目に整理し、問題の構造化をします。構造化することで、問題の関係性が明確になり、解決の糸口となります。
川喜田二郎氏の発案した「KJ法」と同じものです。KJ法を作り出した経緯や運用方法については、著書の「発想法」「続・発想法」で述べられています。


発想法そのものは、たくさんの細切れの情報から系統立てた構成を作り出す技術で、川喜多氏は論文の執筆に活用していました。 ある問題や課題をテーマに設定することで、それを多様な面から見て問題構造を露わにするというやり方で品質管理に活かすこともできます。
解決したい問題や、取り組みたい課題などをテーマに設定します。 テーマが決まったら、それについての意見を出し合い、1つ1枚ずつカードに書き出します。 複数人で意見を出し合うと効果的ですが、一人で思いつく限りの意見を出しても構いません。
書き出すカードに決まりはありませんが、後で並び替えのしやすいように情報カードを使用すると扱いやすくなります。



2枚以上のカードをまとめて、新しくまとめ用のカードを追加します。 まとめる際は少ない枚数でまとめるようにします。あまり多くの枚数を一度にまとめると、一段飛ばしで抽象化されてしまい論理が飛躍することがあります。
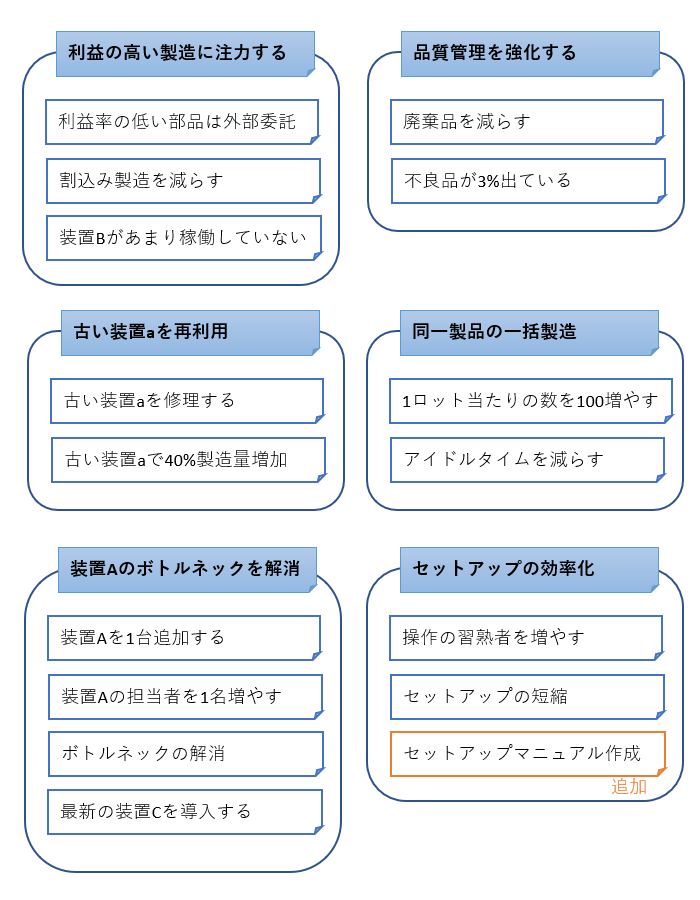
まとめの際に不足している情報や論理的な穴が見つかることがあります。すぐに調べられるものであればカードを追加し、時間がかかるものであれば一旦仮としてまとめ作業を進めます。その場合、後で不足データを調査し、全体の理論に影響があるか確認するようにします。
まとめラベルの内容から更に抽象化を繰り返し、まとめの範囲を徐々に広げていきます。

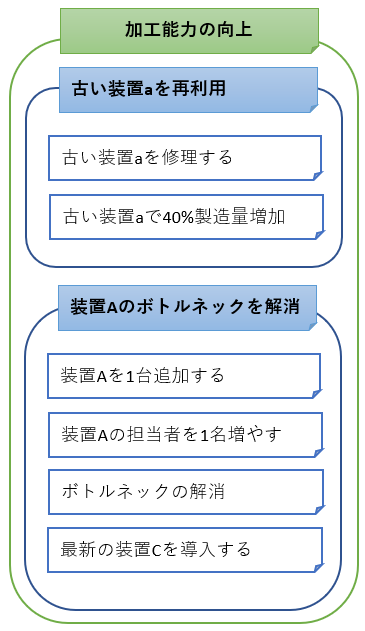
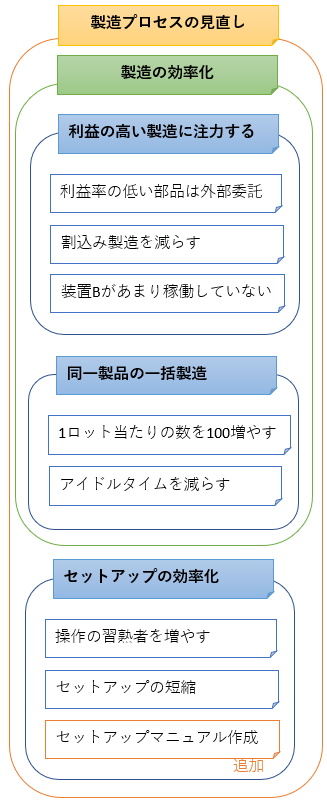
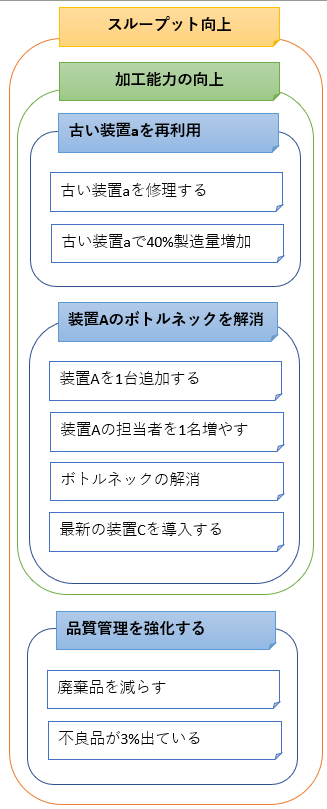
個別の情報が整理されて大きな命題が表れていると思います。 例の図では「製造プロセスの見直し」「重要な加工のスループットを増やす」が命題として表れました。
命題は取り組むべきものを抽象的に表したもので、具体的な改善については費用対効果を考えつつ個々のカードを見直して取り組むべき点を決めます。
課題から要因を掘り下げて、洗い出したものの関係を矢印で結び全体の構造を見えるようにします。 全体構造が見えることで、最も効果的な問題を特定し改善を行います。
沢山の問題を抱えていて、どれから手をつけていいか分からない場合に有効です。 例えば、以下の図は問題が他の問題に影響を与える様子を表しています。
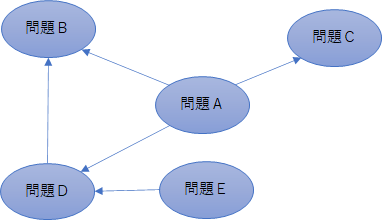
影響を与えることにより、上位の問題が解決されると下位の問題にも解決が波及します。問題Aが解決されると、問題BCDも解決(または改善)されます。
一つだけ問題を解決した場合、波及先も含めて解決される問題の数はこのようになります。
・問題A・・・4つの問題を解決(ABCD)
・問題B・・・1つの問題を解決(B)
・問題C・・・1つの問題を解決(C)
・問題D・・・2つの問題を解決(DB)
・問題E・・・2つの問題を解決(ED)
問題Aを解決することが最も効果的になります。
問題一つ一つの重要性が大きく異なる場合、関係の数ではなく重みづけも加味します。 以下はそれぞれの問題に重要性の重みづけをした図です。
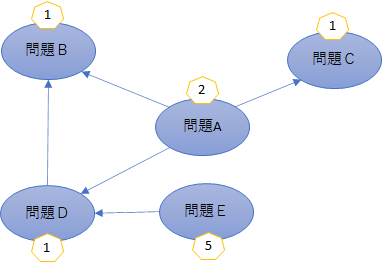
この場合、重みの合計は
・問題A・・・重み5(2+1+1+1)
・問題B・・・重み1(1)
・問題C・・・重み1(1)
・問題D・・・重み2(1+1)
・問題E・・・重み6(5+1)
となり、問題Eを解決することが最も効果的になります。
紙とペンを用意する
紙には要因を一つずつ書くので、ある程度の大きさの紙を用意します。大きめの付箋紙でも構いません。
また、要因を並べてペンで矢印を書くための大きな台紙も必要です。ホワイトボードで代用してもよいです。
人を集める
数人集めてグループで行う事で、多角的な視点から検討することができます。
人数が集められない場合は一人で行うことも可能ですが、知識や理解が無いと後述する要因の深堀が進められない事があります。
用意した紙にテーマや問題を書いて、台紙の中央に置きます。
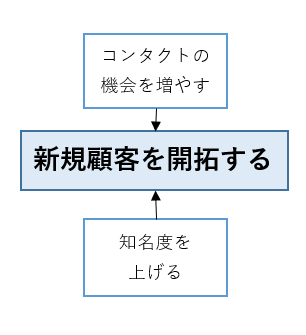
ここでは架空の新規ソフトウェア開発会社が「新規顧客を開拓する」ためにどうすればよいかを考えます。

グループメンバーからテーマや問題に直接連なる要因(一次要因)を出してもらいます。
数が多い場合は3~5つ程度に絞り込みます。
要因は一つずつ紙に書き、中央に置いたテーマの周辺に置きます。
要因からテーマに向かって関係性を表す矢印を書きます。
「2」で出した要因に対し、その要因となるもの(二次要因)を紙に書いて並べます。
こちらも二次要因から一次要因に向かって関係性を表す矢印を書きます。
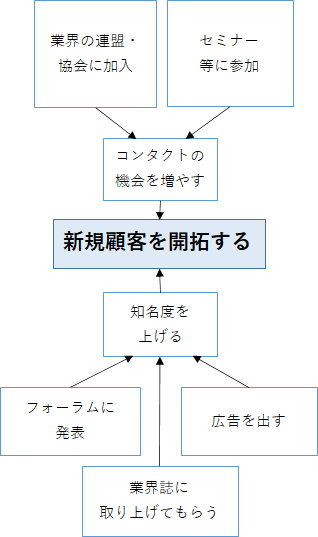
深堀りが十分でなければ更に三次要因、四次要因・・・と深堀りします。
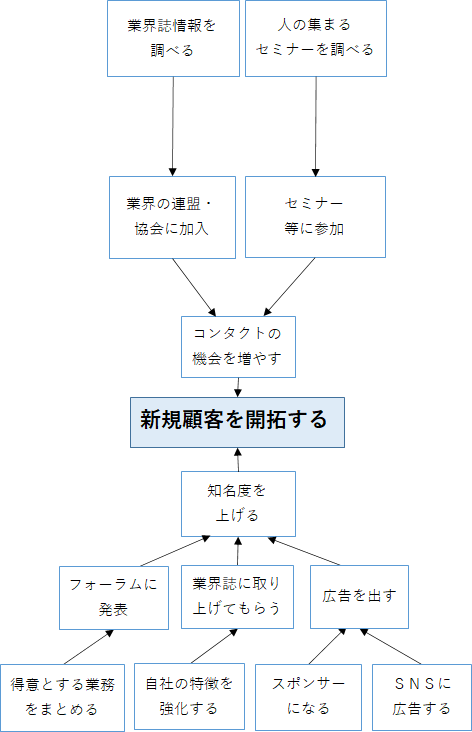
並べてある要因同士に関係があれば、同様に矢印を書きます。
要因間に飛躍や抜けがあれば紙に書いて追加してください。
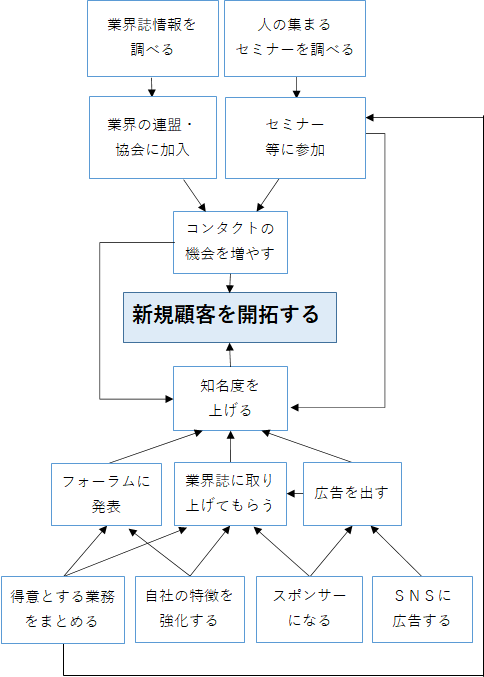
関係の矢印が多く繋がっているものを主要因とします。
要因毎に重みづけをして、その合計点の最も高いものを主要因とする方法もあります。
連関図法の手順としてはここまでです。実際は主要因を取り上げて改善案の検討に進みます。
一つ一つの要因を矢印で結ぶやり方は「ザ・ゴール2」で紹介されているTOCの「現状問題構造ツリー」とよく似ています。 最終的に主要因を特定する点は同じですが、要因を洗い出す手順が異なります。
連関図法・・・要因を深堀することで根源的な要因に辿り着く。
現状問題構造ツリー・・・思いついた問題や課題の関係の中から、影響度合いの大きいものを見つけて重要問題を特定する。
連関図法は深さから、現状問題構築ツリーは広さからアプローチする傾向があります。
次回≫系統図法/ マトリックス図法

