系統図法は木が幹から枝を伸ばしていくように、大元になるものから徐々に細かく分けて見ていく方法です。
系統図法という名前ではなくとも、考え事を整理する際に自然と使った事がある人もいると思います。
要素を分解したり、方策を深堀りすることで、抜けや漏れをなくす事ができます。
系統図法は洗い出しの技術で、そこに並べられた項目の要否や優劣は別途判断する必要があります。
系統図は構成要素展開型と方策展開型の2種類があります。
あるものを構成している要素を、徐々に細かいものへと分解していきます。
現実の物事は複数の要素の組み合わせによってできています。そのため、何か物事を検討する際にそれらを洗い出しておきたい事があります。
例の図は、架空の動物病院が診察した動物の種類を構成要素展開したものです。
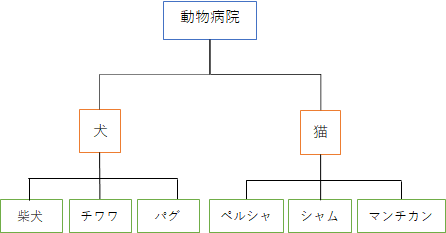
テーマに対する解決方法を、徐々に細かいものへ落とし込んでいきます。
目的から手段、手段から次の手段へと、徐々に細かく具体的な手段を見つけ出していく手法です。
例の図は、架空の従業員Aさんの業務効率が悪い問題を方策展開したものです。
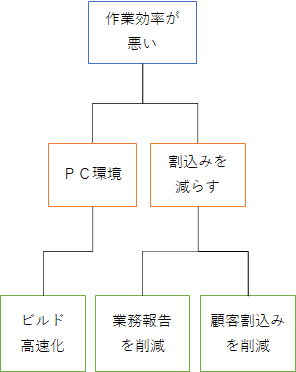
方策展開型で洗い出した問題は、連関図法などで問題の整理・評価を行い、対策手段を選び出します。
マトリックス図法は、数学の行列のように2種類以上の項目を組み合わせたものです。 Microsoft ExcelやGoogle Spread Sheetのように行と列を持つ表計算ツールは、マトリックス図法を簡単に作成することができます。
マトリックス図法は2種類以上の要素の組み合わせが表現しやすいため、品質管理に限らずよく利用されています。また、3種類を組み合わせたマトリックス図法もありますが、読みやすさの点では2種類までの方が優れているため、使用される場面は多くありません。
マトリックス図法は行と列の書き方によって、L型、T型、Y型、X型に分かれます。
行と列の端がくっ付いているマトリックス図法です。
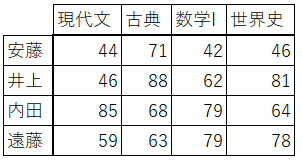
一つのものが複数の要素を持っており、行と列両方の面から要素を比較する場合に便利です。
例の成績表では、生徒の側からみることで特定の生徒の教科別点数を見ることができ、教科の側から見ることで、その教科の点数分布を見ることができます。
要素を左右または上下に分け、その間にもう一つ要素(項目)を配置するマトリックス図法です。
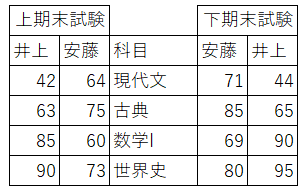
例の成績表では、左側に上期末試験の成績を、右側に下期末試験の成績を、間に試験科目を配置しています。L型マトリックスを2つ合わせたものです。2要素(上期末試験/下期末試験)を1つの図に合わせたことで、要素同士の比較がし易くなります。
Y型は3次元のマトリックスです。立方体で、正面・側面・上面を使って項目を表します。 L型、T型などの2次元マトリックスより複雑なため、使われる頻度は少なくなっています。
有名なものでは、トレッドウェイ委員会組織委員会(COSO)が作成した内部統制のフレームワークであるCOSOキューブにはY型マトリックが使用されています。
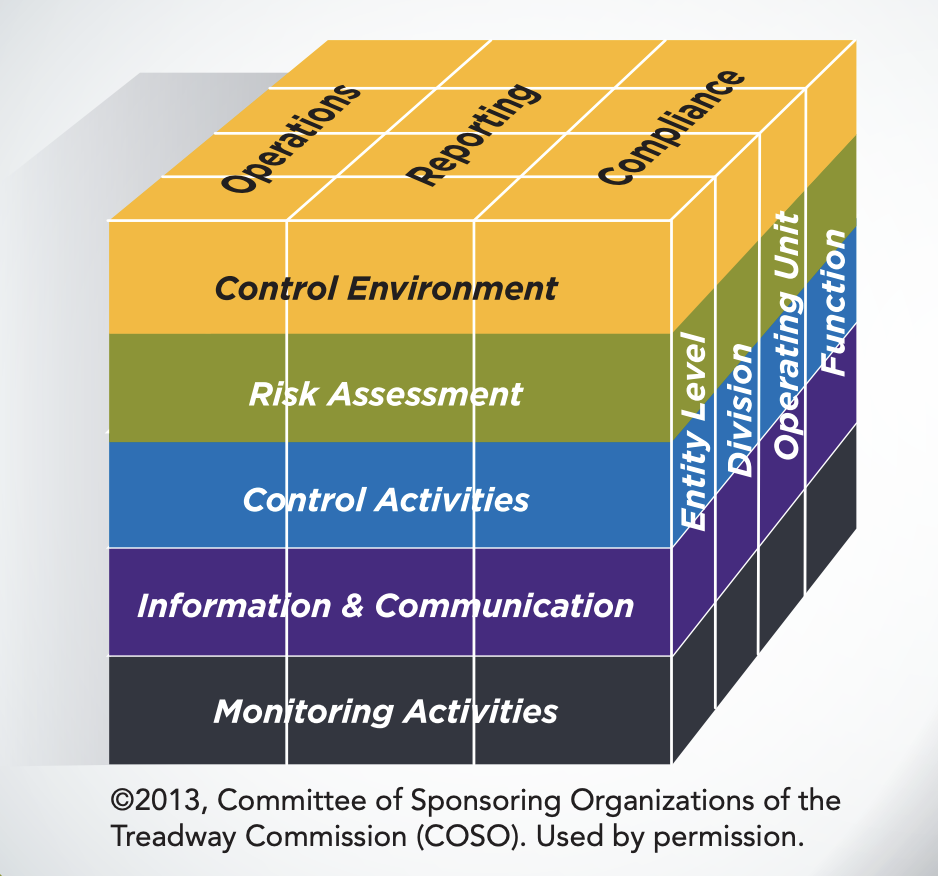
利点としては、A✖️B、A✖️C、B✖️Cを一つの図で表せます。L型マトリックスでは3つの図が必要になりるため、Y型マトリックスの方が簡潔に表現でき、他項目への関係を分かりやすく表すことができます。
欠点としては、1つの項目に対して2つの項目が関係しているため、見た目で理解しにくく、マトリックスの修正・変更が難しくなります。
T型マトリックスはL型マトリックスを2つ合わせたものでしたが、X型マトリックスはT型マトリックスを2つ合わせたものになります。L型マトリックス4つ分です。
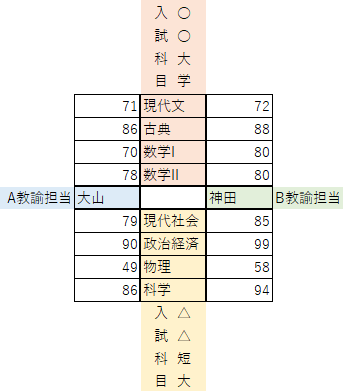
4つの要素が、それぞれ隣り合う2要素に関連している場合に使用します。 例の図では、A教諭とB教諭の担当する生徒が○○大学と△△短大どちらに合格しやすいか、また○○大学と△△短大に合格しやすい生徒がどれくらいいるかを表しています。
マトリックス図法は表計算ツールで書かれることが多いため、L型マトリックスを複数枚の表計算シートに分けて表現していることが多いです。実際の運用でもそれで事足りる場合が殆どなのでL型マトリックス以外を書く機会はあまり無いかもしれません。