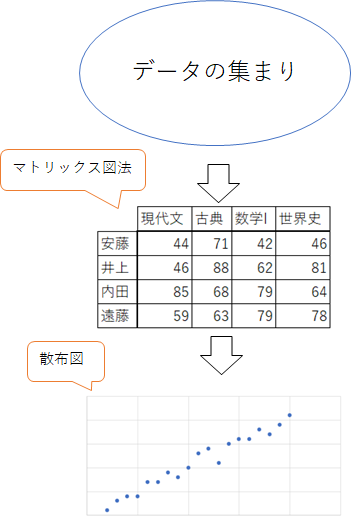
(L型等の)マトリックスデータを元に平面散布図を作成し、散布図の内容からデータの意味を読み解く方法です。
※マトリックス図法と散布図は過去記事にある通りです。
散布図~2項目の関係 https://www.northdetail.co.jp/blog/689/
系統図法/マトリックス図法 https://www.northdetail.co.jp/blog/859
なお、マトリックスデータの要素が2つよりも多い場合、2次元の平面散布図では表せなくなります。その場合は主成分分析を行い平面散布図に落とし込みます。
マトリックス図法は複数要素を持つデータを一覧化する書き方で、データの意味を読み解きやすくしてくれますが、見る人の経験や能力に依存する部分が大きいです。 データの傾向を解釈する散布図までを解析法に含めることで、見る人の能力に左右されることなく、データからその意味するところ読み解くことができるようになります。
スケジュール管理のひとつで、作業にかかる時間・日数と、作業同士の順序を矢印でつないで表したものです。
スケジュール管理の方法にガントチャートがありますが、アロー・ダイアグラムでは作業の相互関係が見えやすくなるため、スケジュール変更による影響が検討しやすいという利点があります。 その反面、ガントチャートよりも作成に手間がかかります。
例として架空のSNSサービスを作成します。 ログインして関連情報を取得し、画面表示を行うまでを対象範囲とします。 一連の機能には以下の工程が必要だとわかりました。
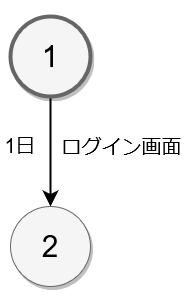
必要な作業を左から右へ進むように並べます。
以下の図は、作業手順1番の「ログイン画面」が「1人」かかり、それを終えると作業手順2番に進むことを表しています。
すべての工程を図にすると、このようになりました。
メッセージと自己情報と画像データの出力すべてが完了して⑧が完了します。
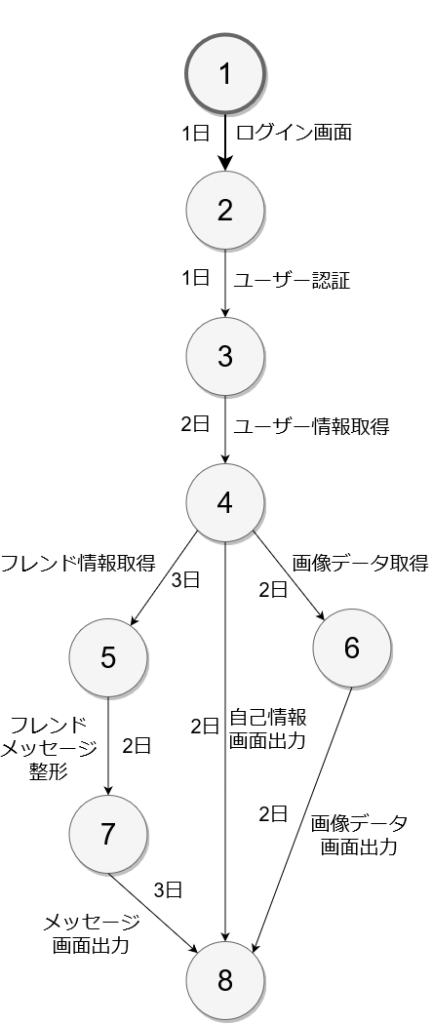
最も早く作業に着手できる日数のことを最早結合点時刻といいます。
例のアロー・ダイアグラム図では、途中で作業が分離するため、ルートが3つ存在しています。
それぞれのルートで、「それまでにかかった日数」+「この作業でかかる日数」を順に足していくと、合計はこのようになります。
1.フレンド情報を出力する作業
作業順序:①→②→③→④→⑤→⑦→⑧
日数合計:1+1+2+3+2+3 = 12
2.自己情報画面出力をする作業
作業順序:①→②→③→④→⑧
日数合計:1+1+2+2 = 6
3.画像データを出力する作業
作業順序:①→②→③→④→⑥→⑧
日数合計:1+1+2+2+2 = 8
⑧はすべての作業が完了している必要があるため、最も日数のかかる12日になります。
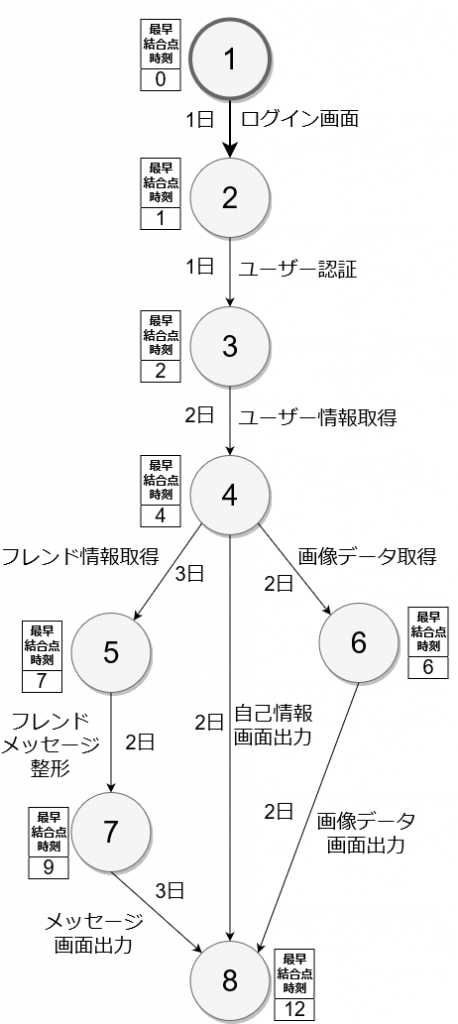
終了時刻を遅れることなく開始できる最も遅い日数(時間)のことを最遅結合点時刻といいます。
最早結合点時刻を計算後、ゴールから逆算していきます。
例のアロー・ダイアグラムでは、すべての作業が完了する⑧の日数(ゴール)が「12日」となっているので、これを元に3つのルートで逆算していきます。
1.フレンド情報を出力する作業
計算順序:⑧→⑦→⑤→④→③→②→①
最遅結合点計算:12-3-2-3-2-1-1
2.自己情報画面出力をする作業
計算順序:⑧→④→③→②→①
最遅結合点計算:12-2-2-1-1
3.画像データを出力する作業
作業順序:⑧→⑥→④→③→②→①
最遅結合点計算:12-2-2-2-1-1
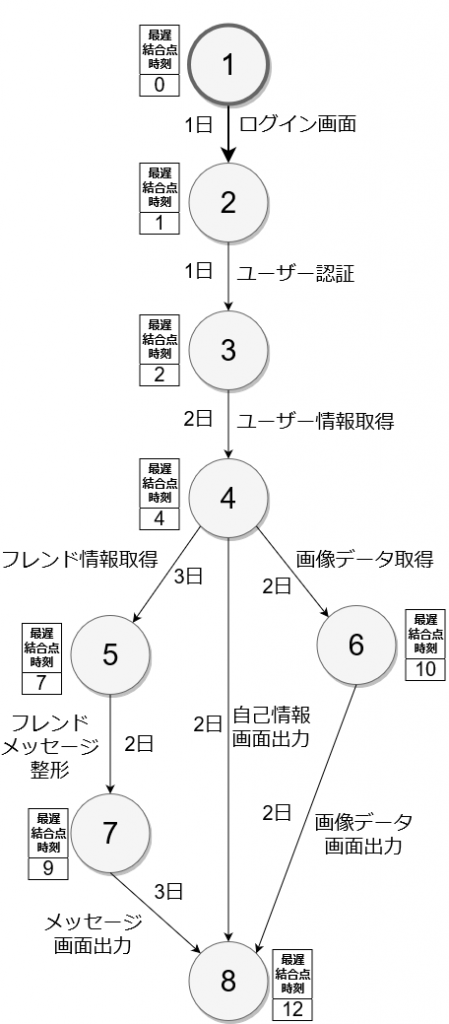
④には3つのルートから到達しますが、ここには最も遅い(日数の残りが少ない)数値が入ります。 フレンド情報出力のルート(⑤→④)では、7日-3日で最遅結合点時刻は4日。
自己情報画面出力のルート(⑧→④)では、12日-2日で最遅結合点時刻は10日。
画像データ出力のルート(⑥→④)では、10日-2日で最遅結合点時刻は8日。
最も遅いルートはフレンド情報出力のルートの4日になるので、④の最遅結合点時刻は4日になります。
作業が遅れても全体のスケジュールに影響が出ない日数を余裕日数といいます。
余裕日数の計算は、各作業の最遅結合点時刻と最早結合点時刻の差分で求めます。
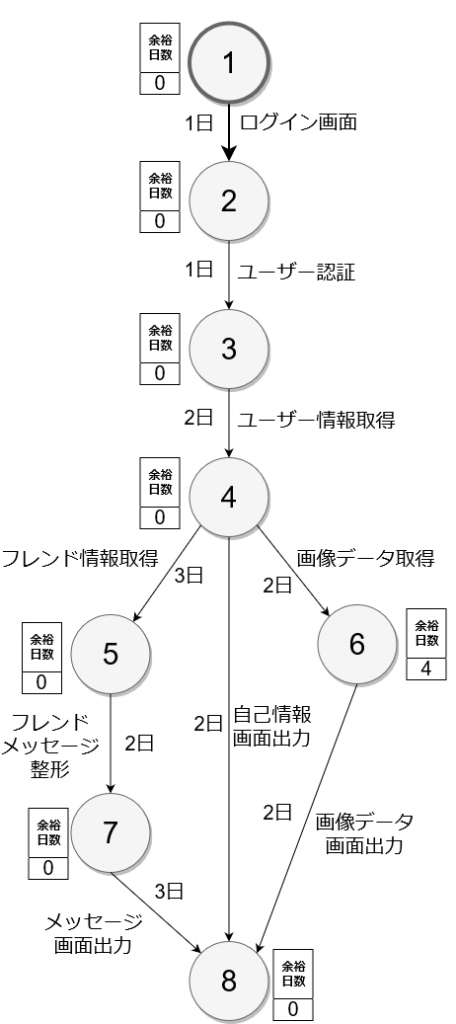
余裕日数が「0」の作業は、遅れるとスケジュール遅延になるクリティカルパスになります。
この図では作業⑥の余裕日数が4日あります。これは作業⑥は予定より4日まで遅延しても、全体のスケジュール遅延にはつながらないことを表しています。
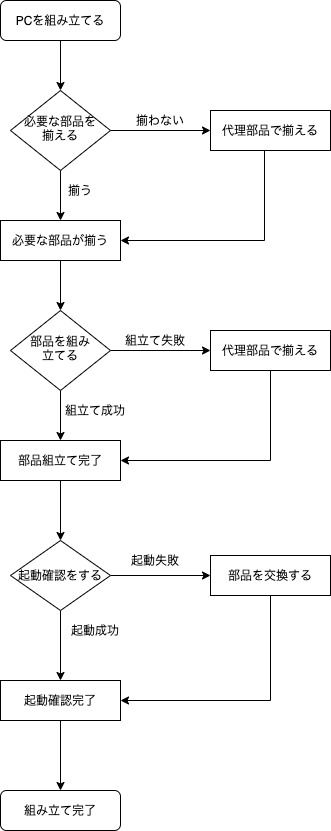
PDPC(Process Decision Program Chart)は日本語にすると過程決定計画図になります。 目標達成までの過程を洗い出してチャートにし、そこで発生しうる問題について対策を用意します。
PDPCには、作成する時期と意図によって逐次展開型と強制連結型の2種類に別れます。どちらもフローチャートを書いて対策を組み込むという点は共通しています。
以下のような手順で行うと作成しやすくなります。
1.メンバーを集める
2.計画のスタートとゴールを決める
3.理想的な計画を書く
4.発生する恐れのある不測の事態を書き加える
5.不測の事態から理想的な計画に戻るための策を考え書き加える
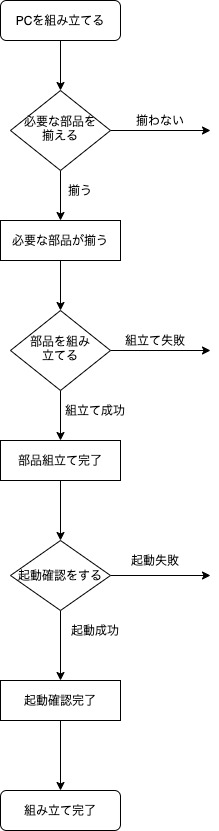
例として、PCをパーツから組み立てる計画を立てたとします。
メンバーとして、PCパーツに詳しいAさん、必要なスペックを決めるリーダーのBさん、調達担当のCさんに集まってもらいました。
スタートは「PCを組み立てる」、ゴールは「組み立て完了」としました。
PC組み立ての理想的な作業の流れをフローチャートにするとこのようになります。